

我的朋友老杨向我咨询一个问题。由于2021年国际海运的运输时间很不稳定,他想要做一下分析,提供给总部作为参考,但不知该如何入手,所以想找我帮忙。
老杨所在的A公司有几家工厂分布在包邮区,通过上海港出口到美国印第安纳州的客户B工厂,主要的运输模式是海运加美国内陆多式联运。货柜抵达美国西海岸的洛杉矶或长滩港后,通过铁路运输至芝加哥,用卡车完成最后的派送。
考虑到启运港都是上海港,老杨统计了从启运港开船到货物送达客户仓库的全部日期,用这个数据来分析运输时间的情况。
A公司的几家工厂出货量并不均衡,有整柜,也有拼柜。有时出货量介于两者之间,老杨也想知道整柜和拼柜的时效性有多少差别。
老杨把2020年11月至2021年10月的实际运输时间提供给我,在经过初步整理后,得出了有效数据共有127条,具体情况如下表。
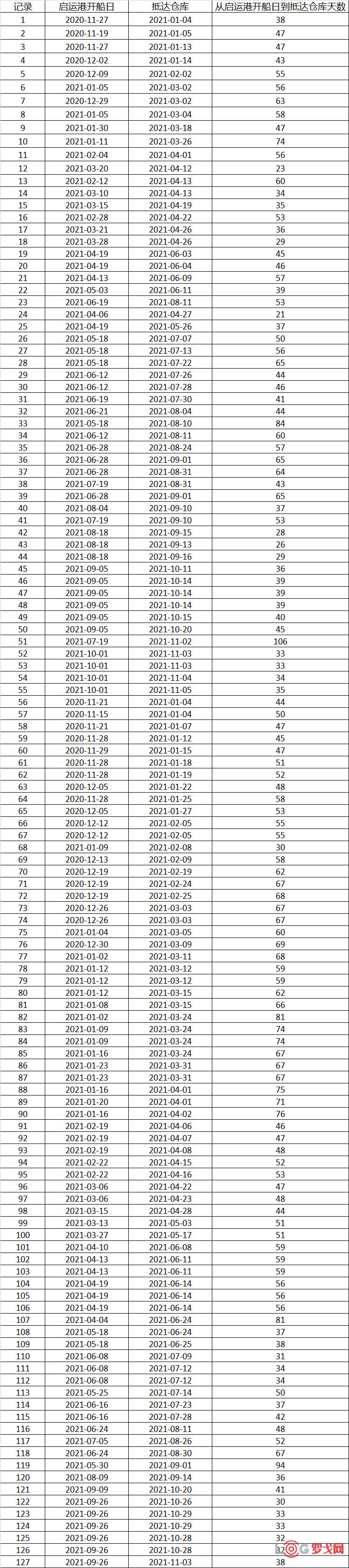
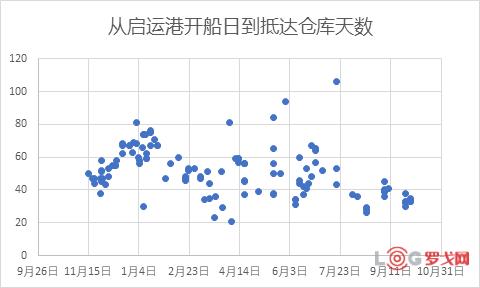
首先使用散点图来看一下,X轴是每票货物实际开船的日期,Y轴是从开船到B公司仓库的总天数,包括了海上运输、进口清关和内陆多式联运的时间。下面的分析都是依照这个统计方式。
初看之下,整体的运输天数在20至105天左右,主要集中在40-60天的区间段。当然目视化的方法只能用于快速判断,我们还要进行下一步的统计分析。
我把数据排序了一下,发现最小值是21天,也就是从上海港至客户仓库最快的时间,这相当厉害了。
但是最大值竟然也有106天,相当于是3. 5个月。最大值和最小值的差距有85天。其中出现次数最多的天数有两个值,也就是众数,分别是47天和67天,各有7次。
想要计算众数,可以使用Excel中的公式MODE.MULT(数值范围),它会返回众数的所有值,我们就不用一个个去数了。
想要知道运输大概率会需要多少天,用平均数是最简单的方法,127条记录的平均数是51天,此处已经四舍五入,下同。
平均数用起来简便,但我们也知道它有缺点,比如上海市平均工资公布后,我总感觉是拖了后腿。因此我们要使用百分位数来分析,当然平均数还是有用的,留在后面再讲。
25百分位数 |
39天 |
50百分位数 |
50天 |
75百分位数 |
60天 |
百分位是指把所有数据从小到大排序,并计算相应的累计百分位。第25百分位数又称第一个四分位数,在我们的统计中有127个记录,25百分位对应的是第31.75,从最小值开始数下来,在第31和第32之间的那个数,也就是39天。
第50百分位数也叫中位数,这个值比平均值更有意义。用75百分位数减去25百分位数的值叫做四分位距,它反映出的是数值之间的间距,体现出一种离散情况。
在这组数据中的四分位距是60-39=21天,意思是从小到大排序数据的第75百分位和第25百分位的差是21天。计算百分位的Excel公式是PERCENTILE.INC(数值范围,百分比) ,比如要计算中位数,就输入0.5。
至此,我们感觉是掌握了一些信息,但还不太够。想要知道这组数据整体偏离平均值的程度,我们要计算一下方差,也就是Variance。
来一波回忆杀,回想当年学过的高中数学吧,方差是各个数据与平均数之差的平方的和的平均数。在这组数据里有127个值,方差的计算公式就是把每个数减去平均数51天后求一个二次方,把所有的平方加起来,再除以127。
在Excel里的计算公式是VAR. S(全部数值),很快就能算出结果是225.31。把方差开个二次根,可以得出标准差是15.01,Excel公式是SQRT(数值)。
看到了这里是不是有点上头了?别着急还有最后一步,我们要算一下变异系数Coefficientof Variation,简称CV。它是用标准差除以平均值,在这里就是15.01/51,等于0.3,这个数字反映了样本数据的离散程度。
一般来说,CV小于0.75说明变化性比较低。我们可以这样理解,虽然运输时间比以前长了,但总体的离散程度很低,说明延长的时间是同比放大了。
只要我们调整在途运输天数的参数,重新计算物料需求计划,由于运输延误造成的缺货风险是总体可控的。这是第一个重要的洞察。
如果我们统计所有发生的运输天数的概率,就可以得到这样一个结果。
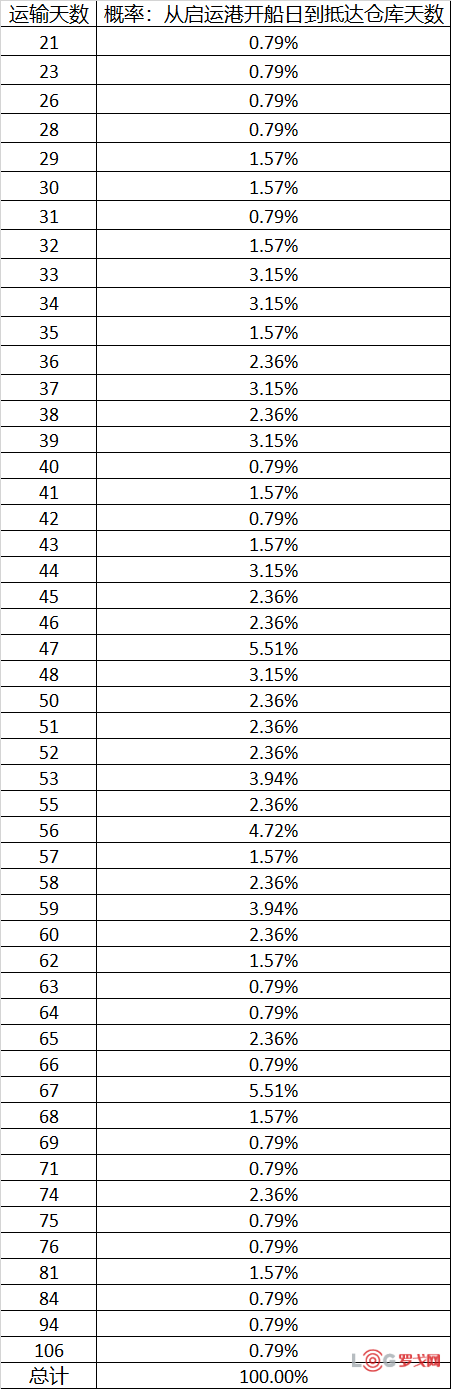
这一步可以在Excel里使用数据透视表完成。选中所有“从启运港开船日到抵达仓库天数”数据。
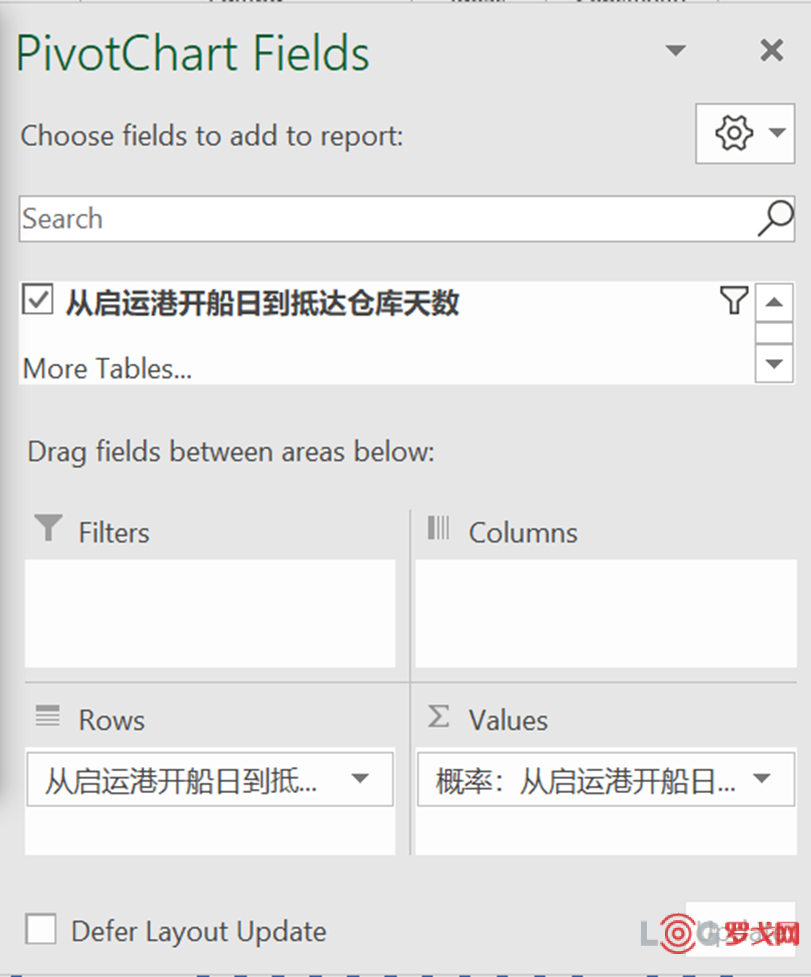
然后在Values里选择Count,在show values as中选择“% of Grand Total”
就可以计算出概率。接下来,使用柱状图把概率展示出来。
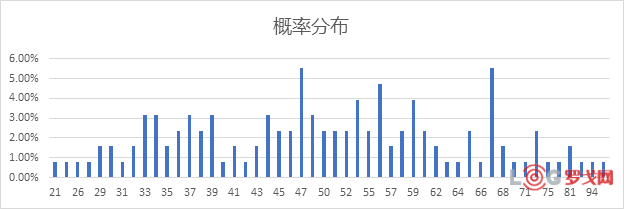
我们之前得出的两个众数,47和67就是Y轴概率最大的两个数,各出现了7次,除以总样本数127,概率就是5.51%。这个分布有点像是正态分布,也有点像是三角形分布,关于这点先放一放,待会儿再来看。
老杨的工厂有时用整柜出货,有时用拼柜。当货物正好装满一个20尺或40尺集装箱的时候,毫不疑问我们应该选择整柜。
但在整柜很难订的时候,我们是否可以化整为零?毕竟市场上的拼柜订舱更加容易一些。在不考虑成本因素的前提下,我们可以先对两种模式的时效性做下分析。
这组数据中有55票整柜,包括20尺和40尺柜,另有72票拼柜,加起来正好是127。我们用之前使用的计算方式,求得了一系列的结果,计算过程不再赘述。
| 数据分析 | 整柜(20FT&40FT) | 拼柜 | 两者之差 |
| 最小值 | 21 | 30 | -9 |
| 众数 | 39 | 67 | -28 |
| 平均值 | 47 | 54 | -7 |
| 25百分位数 | 37 | 45 | -8 |
| 50百分位数 | 45 | 53 | -8 |
| 75百分位数 | 56 | 66 | -10 |
| 最大值 | 106 | 94 | 12 |
| 最大值与最小值的差 | 85 | 64 | 21 |
| 75与25百分位的差 | 19.5 | 21.5 | -2 |
| 方差 | 237.46 | 199.48 | 37.98 |
| 标准差 | 15.41 | 14.12 | 1.29 |
| 变异系数 | 0.33 | 0.26 | 0.06 |
通过比较这两种模式,我们可以得出几个结论。
首先,拼柜的运输时间更长,这是因为货柜在目的地港口需要掏箱,然后再安排零担运输,这会增加运输的总时间,因此这个结果是合理的。
其次,我们发现拼柜的变异系数小于整柜,这说明拼柜虽然慢一些,但时效性比整柜还要稳定,这是另一个重要洞察。
如果我们把整柜和拼柜的概率分布拿出来看一下,它们展示出来的情况如下:
1.整柜的分布
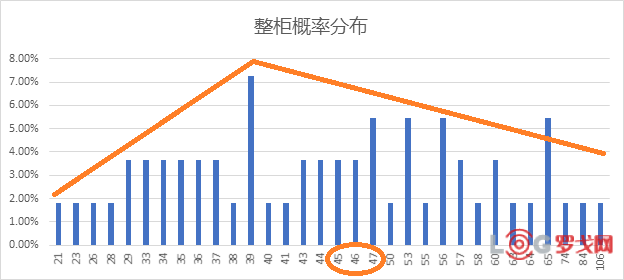
这个分布呈现出了三角形分布的特征,众数39是整组数据的概率最大值,其他概率在“39”的左右不均衡地分布着,中位数45和平均值47都在它右侧。
2.拼柜的分布
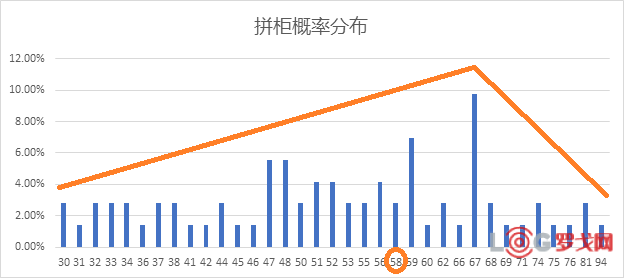
拼柜同样地出现了三角形分布,众数67是该组数据的概率最大值,其他概率在它的左右不均衡地分布着。这次中位数53和平均值54都在67的左侧,这与整柜的情况是相反的。
我们不去深究为什么会造成这两种情况,只需要知道三角形分布很适用于运输时间概率分析就好了。
在这样的场景中,正态分布未必是最合适的,因为运输时间的最小值是有极限的,比如21天,但是最大值可能会超乎预期,只要在整个运输环节中的任意一点脱节,就会造成难以预料的延误,最大值106天就是一个例证。
如果不幸遇到了苏伊士运河堵塞的情况,那么最大值就又要无限期地增加了,概率分布应该不是正态分布,而是三角形分布了。
通过对这些数据的分析,我们至少可以得出以下的几个结论。
1.运输时间
新冠疫情引发的一系列问题,属实增加了海运的运输时间。同时我们也发现变异系数还是较低的,不管是整柜还是拼柜。定期回顾实际运输时间,然后在系统里调整前置时间参数,就可以避免因运输延误造成的逾期订单或缺货。
2.整柜和拼柜的时效性
综合来看,整柜虽然比拼柜更快一些,但是没有拼柜时效性稳定,前者的变异系数甚至更多了6%。整柜虽然没有在堆场拆箱,二次运输的过程,但依然卡在了其他多式联运的环节上,并没有体现出优势。
拼柜是一个很好的备选方案,优势是不用等柜子,因为是和其他出货人共享集装箱,更容易获得舱位和可能更早的船期。
3.前提假设
以上结论仅是基于A公司和它所选择的货代,运输至美国B公司的场景下得出的结论,并不一定适用于其他场景,但这套方法论是可以供借鉴的。
供应链的本质就是数学,用数据说话,拒绝无意义的空谈。使用数据分析,可以帮助我们穿越迷雾,洞察供应链的真相。

UPS卖掉货运后,FedEx也考虑剥离货运,全球公路货运寒冬?
4792 阅读
公交车送快递,邮政、顺丰、京东物流等巨头纷纷入局
2319 阅读
8家快递被曝有一半“向上取整”!快递违规收费全清单!
1401 阅读41页PPT深度解读京东物流一体化供应链模式!
1216 阅读京东物流智狼机器人跑向全国!拣货最快秒级
1206 阅读DPD英国与Yeep!达成战略合作 将新增8000个自提柜
1007 阅读浙江省开通首条往返乌兹别克斯坦全货机航线
1014 阅读链库与新疆海鸿冷链达成战略合作
889 阅读马士基与沙特邮政建立战略合作伙伴关系
875 阅读轩航国际航空物流(深圳)有限公司完成2000万人民币A轮融资
922 阅读